الموضوعات الرياضية التي يتناولها الطلاب خلال مراحلهم الدراسية تتضمن جوانب متنوعة من علم الهندسة بما في ذلك الهندسة الفراغية التي تُعد من أبرز فروع الرياضيات نظرًا لاهتمامها بحساب المساحات والأحجام والعمل على قياس الأبعاد المختلفة مثل الطول والعرض والارتفاع والعمق وذلك استنادًا إلى مجموعة من النظريات والخصائص التي تتعلق بالمجسمات ثنائية الأبعاد والتي تقوم بتحديد طبيعة الأسطح في الأشكال ثلاثية الأبعاد مثل المكعب ومتوازي المستطيلات والمخروط والمنشور والهرم والأسطوانة.
عدد عناصر الأسطوانة من أوجه وأحرف ورؤوس
- الأسطوانة تُعد أحد الأشكال الهندسية الأساسية التي يتم تدريسها ضمن المناهج التعليمية للطلاب في مختلف المراحل الدراسية.
- لذلك يكثر التساؤل حول عدد الأوجه والأحرف والرؤوس التي تتكون منها الأسطوانة والإجابة الدقيقة على هذا السؤال هي أنها لا تحتوي على أي رؤوس أو أحرف ولكن تمتلك وجهين فقط.
مفهوم الأسطوانة بأسلوب مبسط
- الأسطوانة تُصنَّف ضمن الأشكال الهندسية ثلاثية الأبعاد، وتتميز بوجود سطح منحنٍ دون زوايا أو حواف حادة كما هو الحال في بعض الأشكال الهندسية الأخرى.
- جميع النقاط الواقعة على سطحها الخارجي تمتلك المسافة ذاتها من المحور المركزي، مما يمنحها مظهرًا متناظرًا ومتوازنًا.
- المحور الذي يصل بين مركزي القاعدتين يُمثّل العمود الذي تستند إليه الأسطوانة في بنيتها.
- عند لف مستطيل حول أحد أضلاعه بطريقة دائرية متصلة، نحصل على شكل هندسي مغلق يشبه الأسطوانة.
- يُطلَق على هذا المحور محور دوران المستطيل، بينما الضلع المقابل له هو الذي يتحكم في قياسات الأسطوانة من حيث أبعادها وشكلها النهائي.
أهم السمات المميزة للأسطوانة
على الرغم من أن الأسطوانة لا تحتوي على رؤوس ولها حافتان فقط إلا أنها تُعد من الأشكال الهندسية التي تتمتع بخصائص فريدة تُميزها عن غيرها من المجسمات ومن بين هذه الخصائص:
- تتكون الأسطوانة من قاعدتين إحداهما في الأعلى والأخرى في الأسفل.
- هاتان القاعدتان عبارة عن دائرتين متطابقتين ومتقابلتين يقع مركز كل منهما على نفس المحور كما أن لكل منهما نصف القطر نفسه.
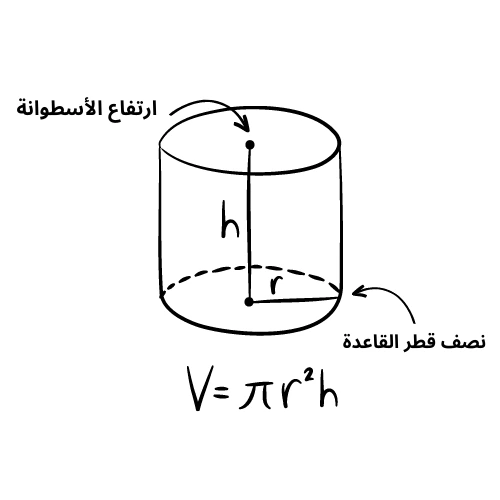
- يُطلق على القطعة المستقيمة التي تصل بين القاعدتين بشكل عمودي اسم ارتفاع الأسطوانة وإذا كان هذا الارتفاع متعامدًا تمامًا على القاعدتين فإن الأسطوانة تُعرف بالأسطوانة القائمة.
- أما إذا لم يكن هذا الارتفاع متعامدًا على القاعدتين بل على إحداهما فقط فتُعرف في هذه الحالة بالأسطوانة المائلة.
- إذا كان المقطع العرضي للأسطوانة يأخذ شكل أحد القطوع المخروطية مثل القطع المكافئ أو القطع الناقص أو القطع الدائري الكامل فإنها تُسمى وفقًا لهذا المقطع كأن نقول الأسطوانة المكافئة أو الأسطوانة الناقصة أو الأسطوانة الكاملة تبعًا للشكل الناتج.
- تماثل الأسطوانة المنشور في أن كلًا منهما يحتوي على مقطع عرضي ثابت في جميع نقاطه على امتداد ارتفاعه.
- تأخذ القاعدتان في الأسطوانة أشكالًا مختلفة فقد تكون دائرية أو بيضاوية وتُسمى الأسطوانة وفقًا لشكل القاعدة أي الأسطوانة الدائرية أو البيضاوية بحسب التصميم.
- يتم حساب المساحة الكلية للأسطوانة من خلال جمع مساحة سطحها الجانبي مع مجموع مساحتي القاعدتين.
القوانين الأساسية التي تستند إليها الأسطوانة
عند الحديث عن الأسطوانة نجد أنها كغيرها من الأشكال الهندسية تعتمد على قوانين محددة لحساب مساحتها وحجمها ولا يمكن إجراء أي حسابات صحيحة دون معرفة هذه القوانين الأساسية التي تشمل:
- حجم الأسطوانة يعتمد على العلاقة بين مساحة القاعدة والارتفاع ويُحسب باستخدام المعادلة التالية.
- حجم الأسطوانة = مساحة قاعدة الدائرة × الارتفاع.
- عند التعبير عنها بالرموز تصبح.
- حجم الأسطوانة = π × مربع نصف قطر القاعدة × ارتفاع الأسطوانة أي.
- = (π × نق²) × (ع).
- حيث أن.
- الرمز “نق” يشير إلى نصف قطر القاعدة الدائرية.
- الرمز “ع” يُمثل ارتفاع الأسطوانة.
- مساحة الأسطوانة يتم حساب مساحتها الكلية من خلال جمع مساحات مكوناتها المختلفة وفق الصيغة التالية.
- مساحة الأسطوانة = مجموع مساحة القاعدتين + المساحة الجانبية المتمثلة في المستطيل.
- بما يعني: مساحة الأسطوانة = 2 × (π × نق²) + 2 × π × نق × ع.
- وفقًا للرموز نجد أن: “نق” يرمز إلى نصف قطر القاعدة الدائرية.
- و”ع” يُمثل ارتفاع الأسطوانة.
الفروقات بين شكل المخروط وشكل الأسطوانة
عند مقارنة الشكلين الهندسيين المخروط والأسطوانة يمكن ملاحظة أوجه التشابه والاختلاف بينهما من حيث البنية الهندسية وبعض الخصائص ويتضح ذلك بشكل أدق عند استعراض الفروقات بينهما وفق الجدول التالي:
الاسم بالإنجليزية:
- Cylinder.
- Cone.
التعريف:
- عبارة عن مجسم ينتج عند تدوير المستطيل حول أحد أضلاعه دورة كاملة ويتميز بوجود محور مركزي يُعرف بمحور الأسطوانة.
- مجسم هندسي ذو قاعدة دائرية مسطحة ويُلاحظ أنه ينتهي بنقطة حادة تُعرف برأس المخروط.
عدد الأحرف:
- لا يحتوي على أي أحرف.
- لا يمتلك أي أحرف أيضًا.
عدد الرؤوس:
- لا يوجد له رؤوس.
- يحتوي على رأس واحدة فقط.
عدد الأوجه:
- يتكون من وجهين.
- يحتوي على وجه واحد فقط.